qacReg for Logistic Regression

In this analysis, we’ll develop a model for predicting births by caesarian from patient characteristics uing the caesarian data frame.

Model fitting is normally an iterative process. We’ll skip this to keep things simple.

Fit the model 

library(qacReg)
data(caesarian)

fit <- glm(caesarian ~ ., family = binomial, data = caesarian)

# or
# fit <- regress(caesarian ~ ., data = caesarian)

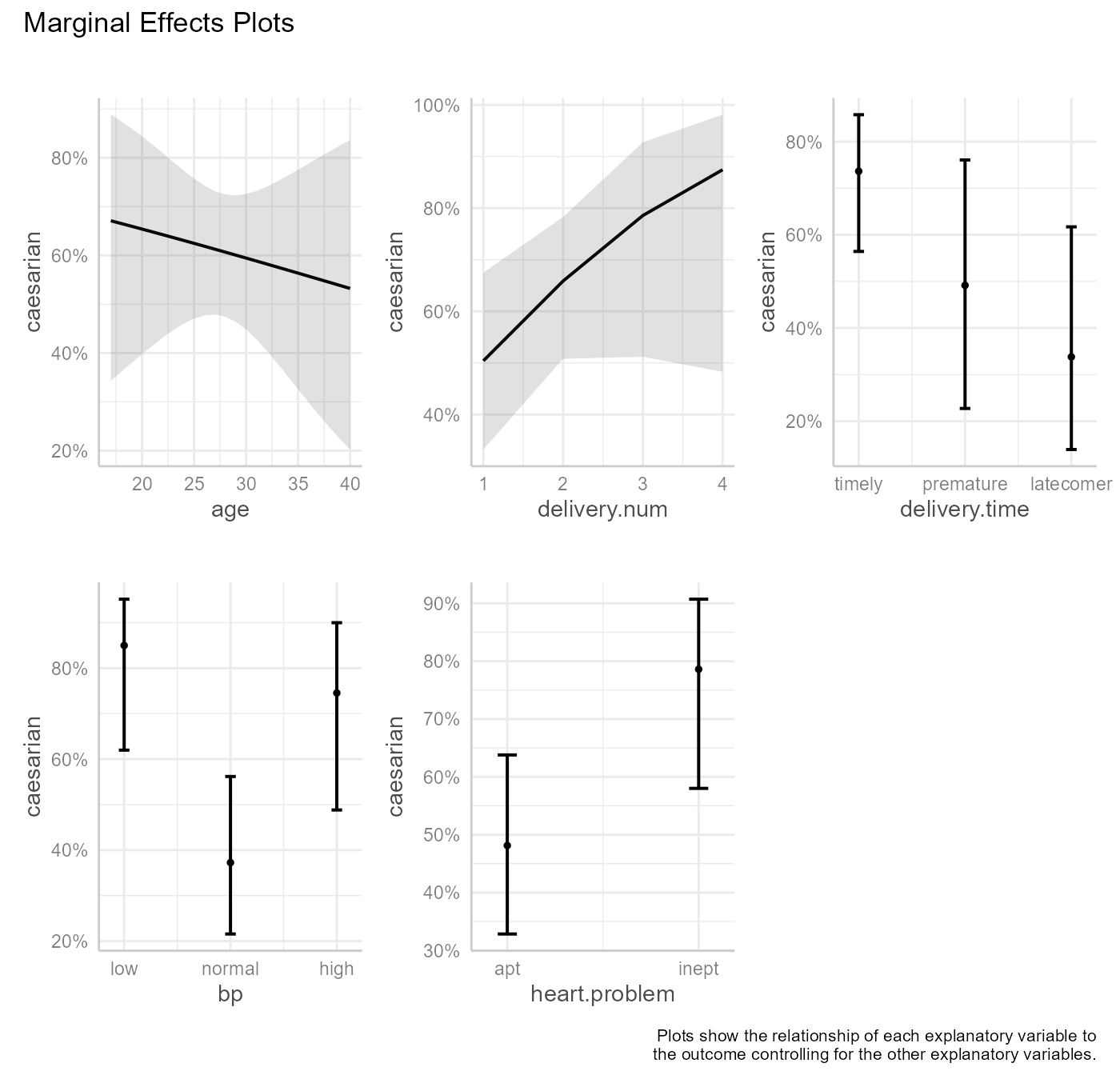
Examine the model 

info(fit)
#> LOGISTIC REGRESSION SUMMARY 
#> Formula: caesarian ~ .
#> Data   : caesarian
#> N      : 80
#> 
#> Predicted category: yes
#> 
#> Omnibus Test 
#> Chi-square(7) = 24.5557, p = 0.0009094 ***
#> 
#> Fit Measures 
#> Stukel's GOF Test: Chi-square(2) = 2.7587, p < 0.2517
#> Tjur's Psuedo-R.squared: 0.2715
#> AIC: 100.541 
#> 
#> Anova Table (type III tests) 
#>               LR Chisq DF Pr(>Chisq)   
#> age             0.1874  1   0.665107   
#> delivery.num    2.6039  1   0.106598   
#> delivery.time   6.3377  2   0.042052  *
#> bp             10.9374  2   0.004217 **
#> heart.problem   5.6196  1   0.017761  *
#> 
#> Logistic Regression Coefficients 
#>                               B      SE       z Pr(>|z|)   
#> (Intercept)             1.43912 1.60133  0.8987 0.368811   
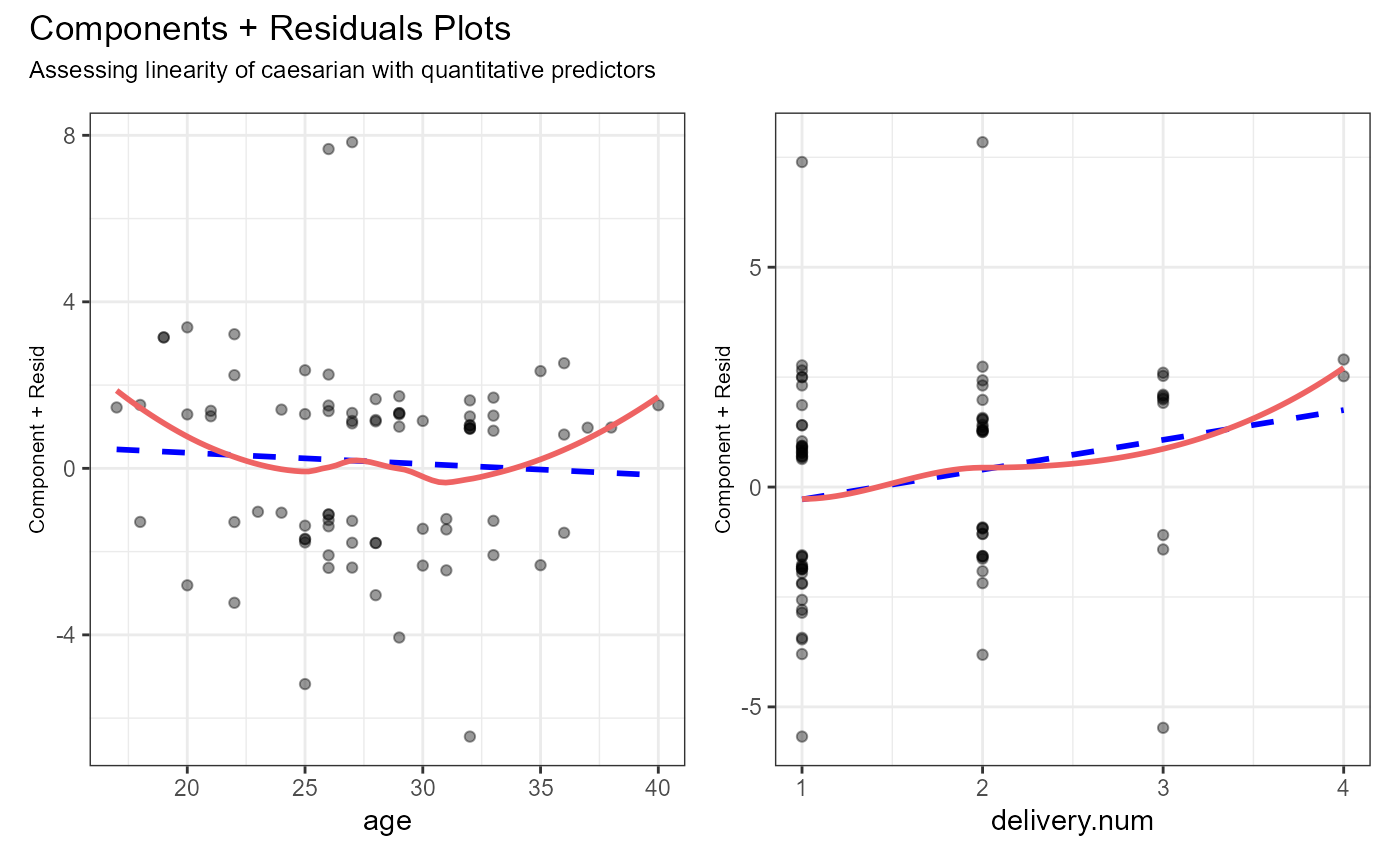
#> age                    -0.02534 0.05883 -0.4307 0.666678   
#> delivery.num            0.64139 0.41054  1.5623 0.118218   
#> delivery.timepremature -1.06162 0.73059 -1.4531 0.146193   
#> delivery.timelatecomer -1.70004 0.74871 -2.2706 0.023170  *
#> bpnormal               -2.25423 0.79667 -2.8296 0.004661 **
#> bphigh                 -0.65859 0.80363 -0.8195 0.412491   
#> heart.probleminept      1.37590 0.60431  2.2768 0.022797  *
#> 
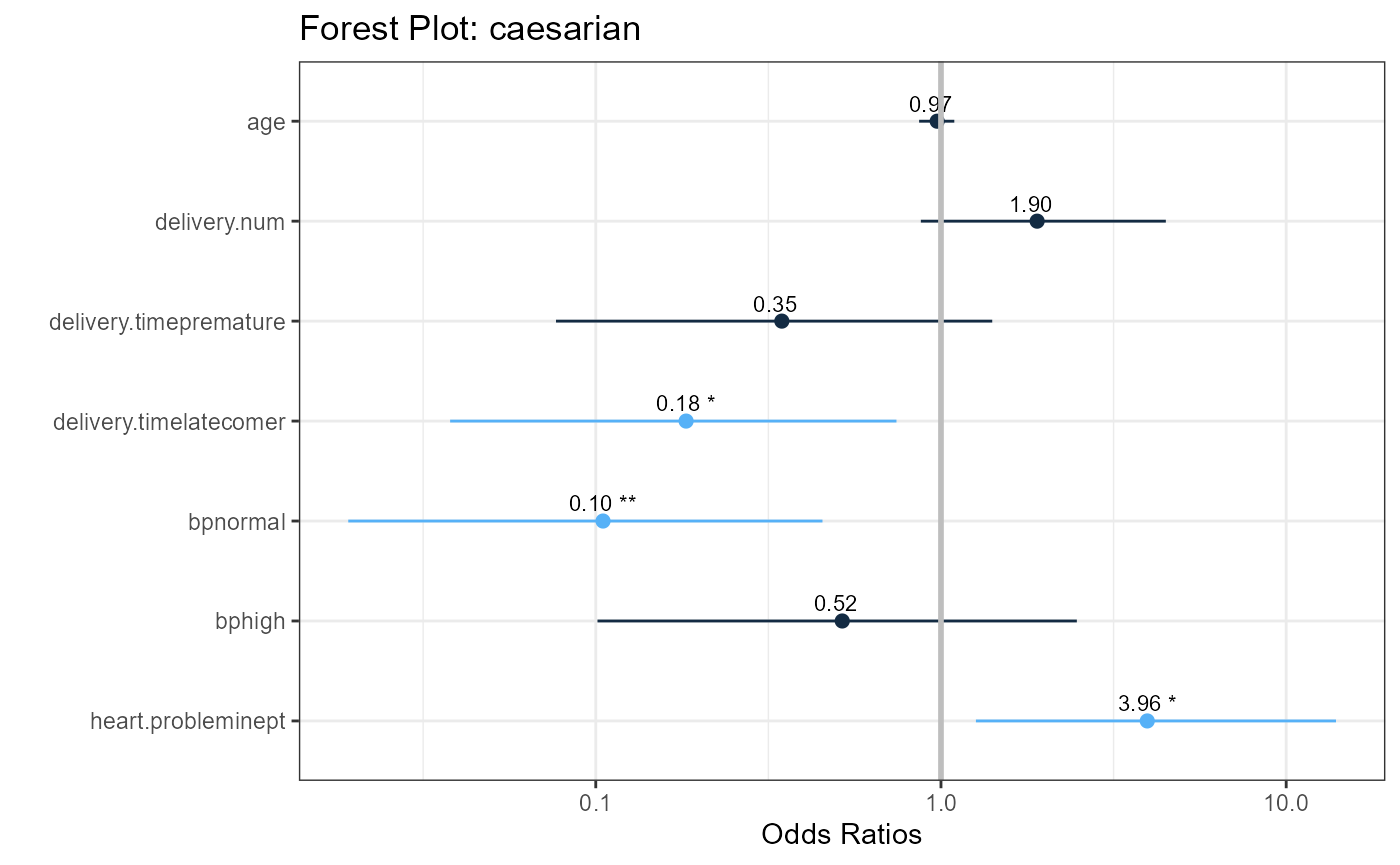
#> Odds Ratios (with 95% Confidence Intervals) 
#>                        Odds Ratio    2.5%   97.5%
#> age                        0.9750 0.86430  1.0930
#> delivery.num               1.8991 0.87428  4.4808
#> delivery.timepremature     0.3459 0.07670  1.4076
#> delivery.timelatecomer     0.1827 0.03786  0.7431
#> bpnormal                   0.1050 0.01919  0.4536
#> bphigh                     0.5176 0.10116  2.4749
#> heart.probleminept         3.9586 1.26252 13.9405

Perform regression diagnostics

Visualize the model parameters

Evaluate variable importance 

relimp(fit)
#> working ...

Assess predictive performance 

performance(fit)
#> LOGISTIC REGRESSION PERFORMANCE 
#> Data              : caesarian 
#> N                 : 80 
#> Response variable : caesarian 
#> Category Balance  : no (0.42%) yes (0.58%) 
#> Predicted category: yes 
#> Prob to classify  : >=0.5
#> 
#> Model: glm(caesarian ~ .,
#>            family = binomial, data = caesarian)
#> 
#> Confusion Matrix 
#> 
#>          Actual
#> Predicted no yes
#>       no  22  11
#>       yes 12  35
#> 
#> Overall Statistics 
#> 
#> Accuracy: 0.7125 
#> 97% CI  : (0.6005, 0.8082)
#> No Information Rate:  0.575 
#> P-Value [Acc > NIR]:  0.007869 
#> 
#> Statistics by Category 
#>                      
#> Sensitivity    0.7609
#> Specificity    0.6471
#> Pos Pred Value 0.7447
#> Neg Pred Value 0.6667
#> F1             0.7527
#> ---
#> Note: recall = sensitivity, 
#>       precision = pos pred value.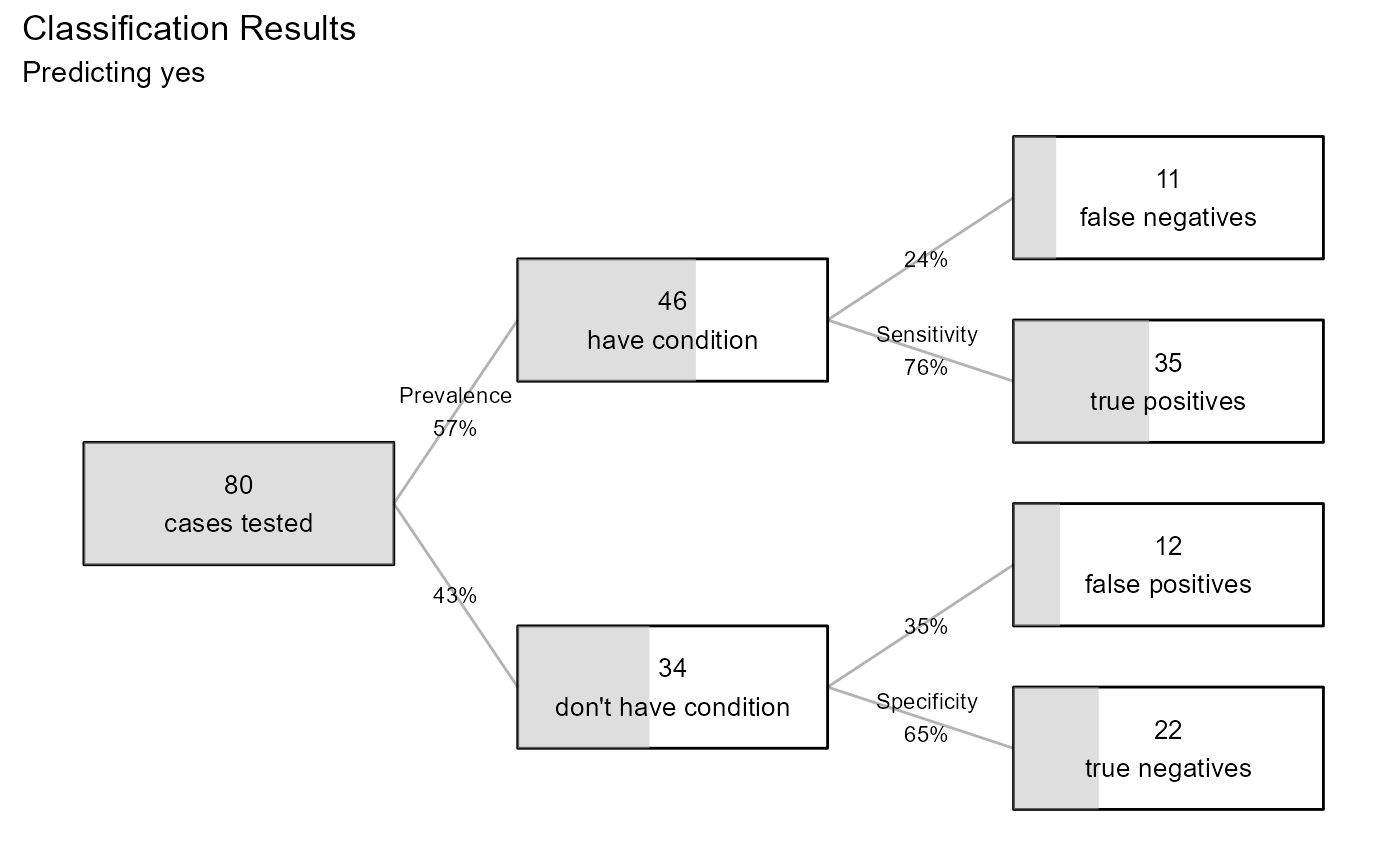

Additional output

ROC Plot 

pred <- predict(fit, caesarian, type="response")
roc_plot(caesarian$caesarian, pred, positive="yes")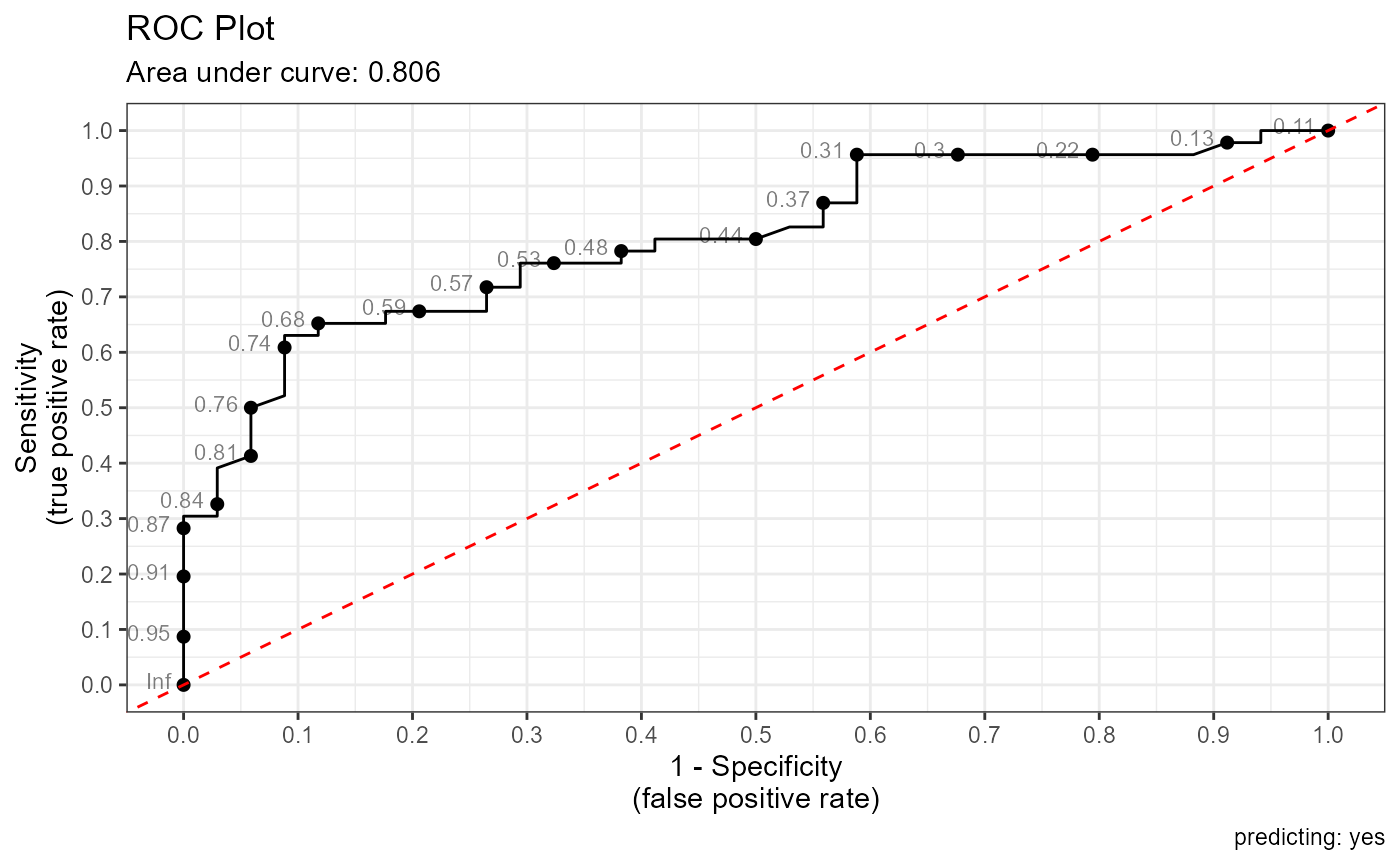

Lift and Gain Charts 

lift_plot(caesarian$caesarian, pred, positive="yes")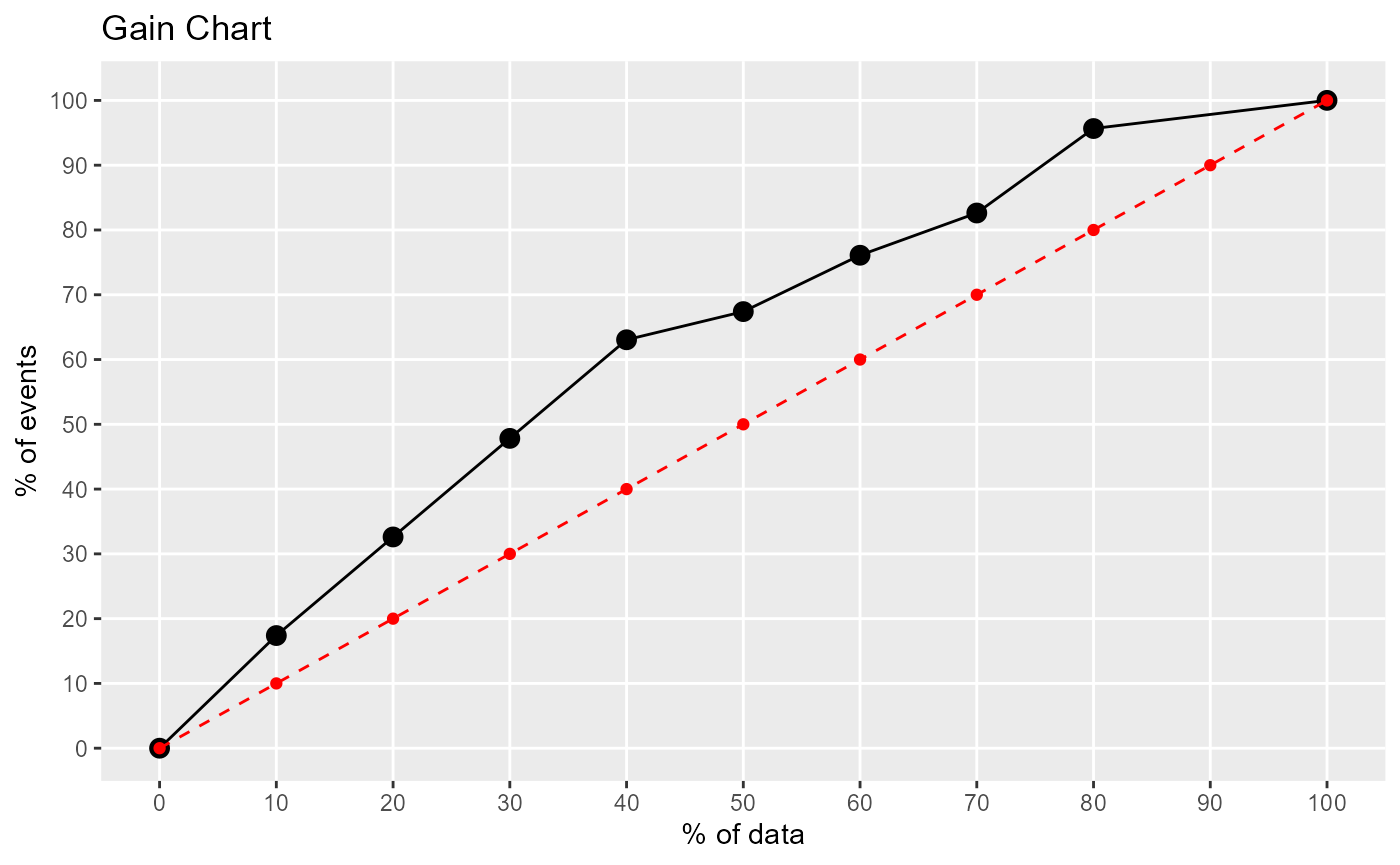

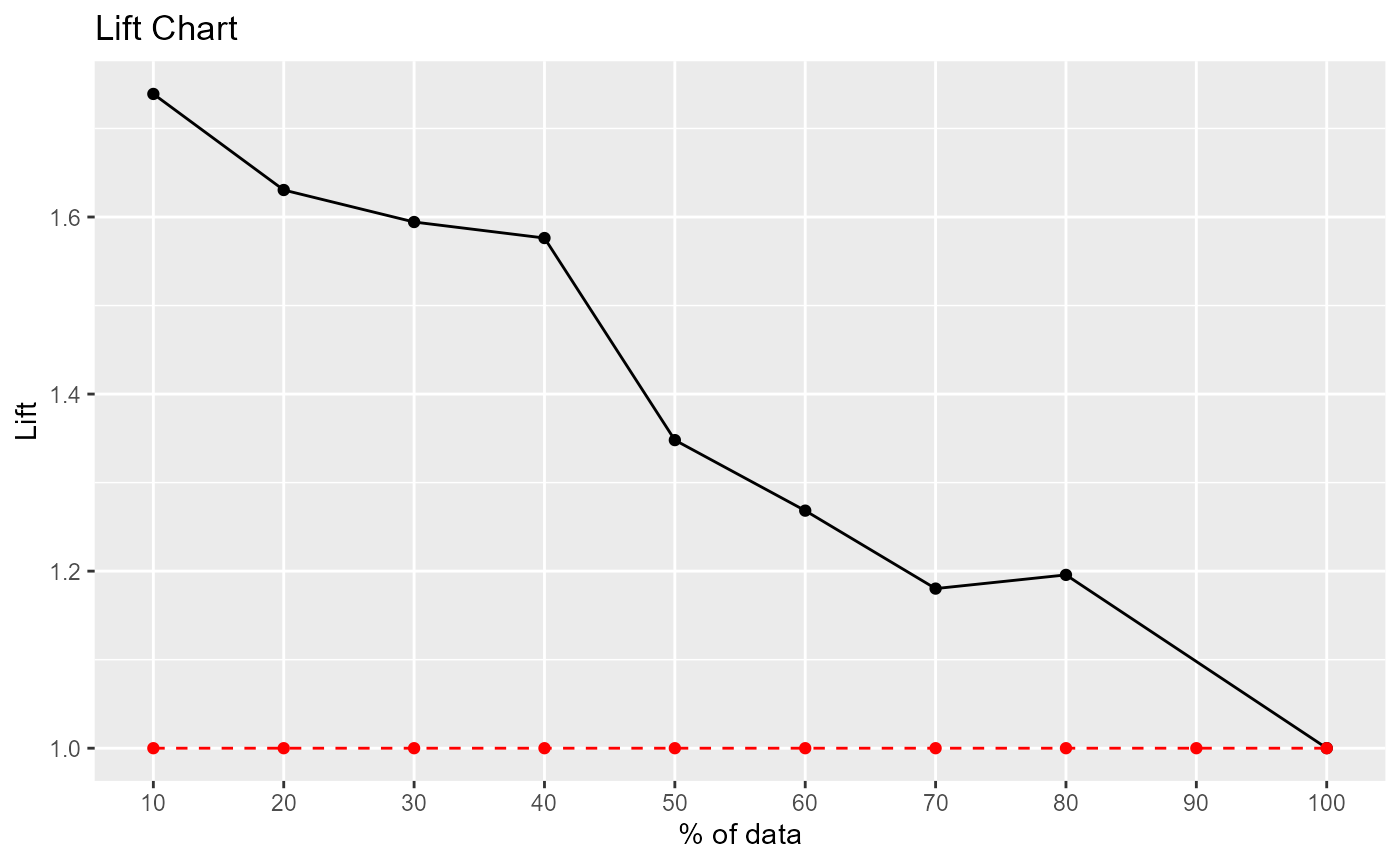
#>   decile ncases nresp cumresp pctevents   gain  cumlift
#> 1     10      8     8       8     17.39  17.39 1.739000
#> 3     20      8     7      15     15.22  32.61 1.630500
#> 4     30      8     7      22     15.22  47.83 1.594333
#> 5     40      8     7      29     15.22  63.05 1.576250
#> 6     50      8     2      31      4.35  67.40 1.348000
#> 7     60      8     4      35      8.70  76.10 1.268333
#> 8     70      8     3      38      6.52  82.62 1.180286
#> 9     80      8     6      44     13.04  95.66 1.195750
#> 2    100      8     2      46      4.35 100.01 1.000100