Principal Components Analysis

Source: R/pca.R

PCA performs a principal components analysis

PCA(data, nfactors = NULL, rotate = "none", digits = 2, ...)

Arguments

data

a data frame or correlation matrix.
nfactors

nuber of factors to extract.
rotate

factor rotation to perform.
digits

number of digits to retain.
...

parameters passed to the psych::principal function.

Value

returns a list with 5 components:

call

the call

loadings

structure matrix

variance

variance accounted for

phi

component intercorrelations for oblique rotations

scores

component scores if factors are extracted from a data frame

Details

The PCA function is a wrapper for the psych::principal function. Component rotations include none, varimax, and promax.

See also

FA, plot.factorAnalysis, score, and scree_plot.

Examples

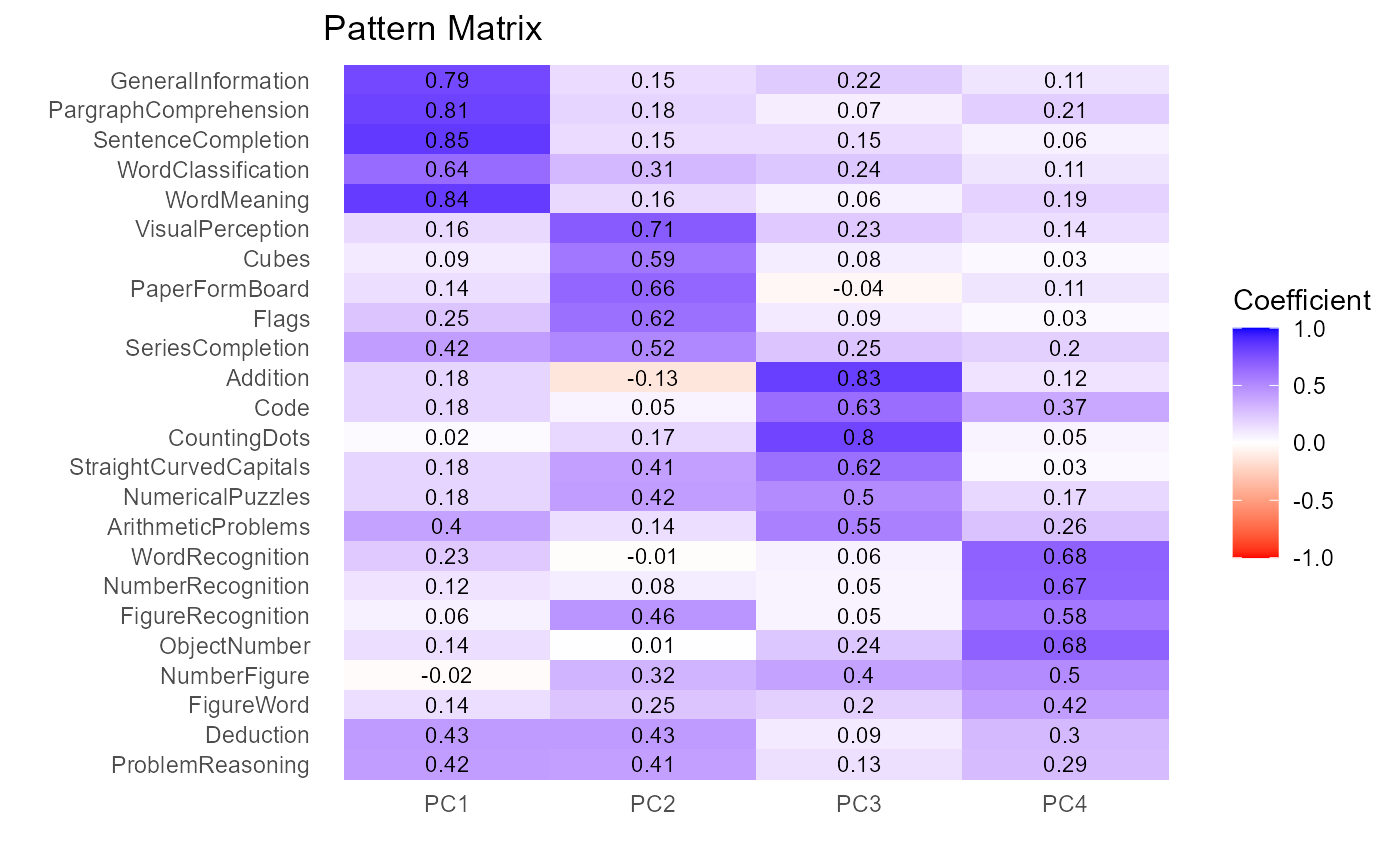
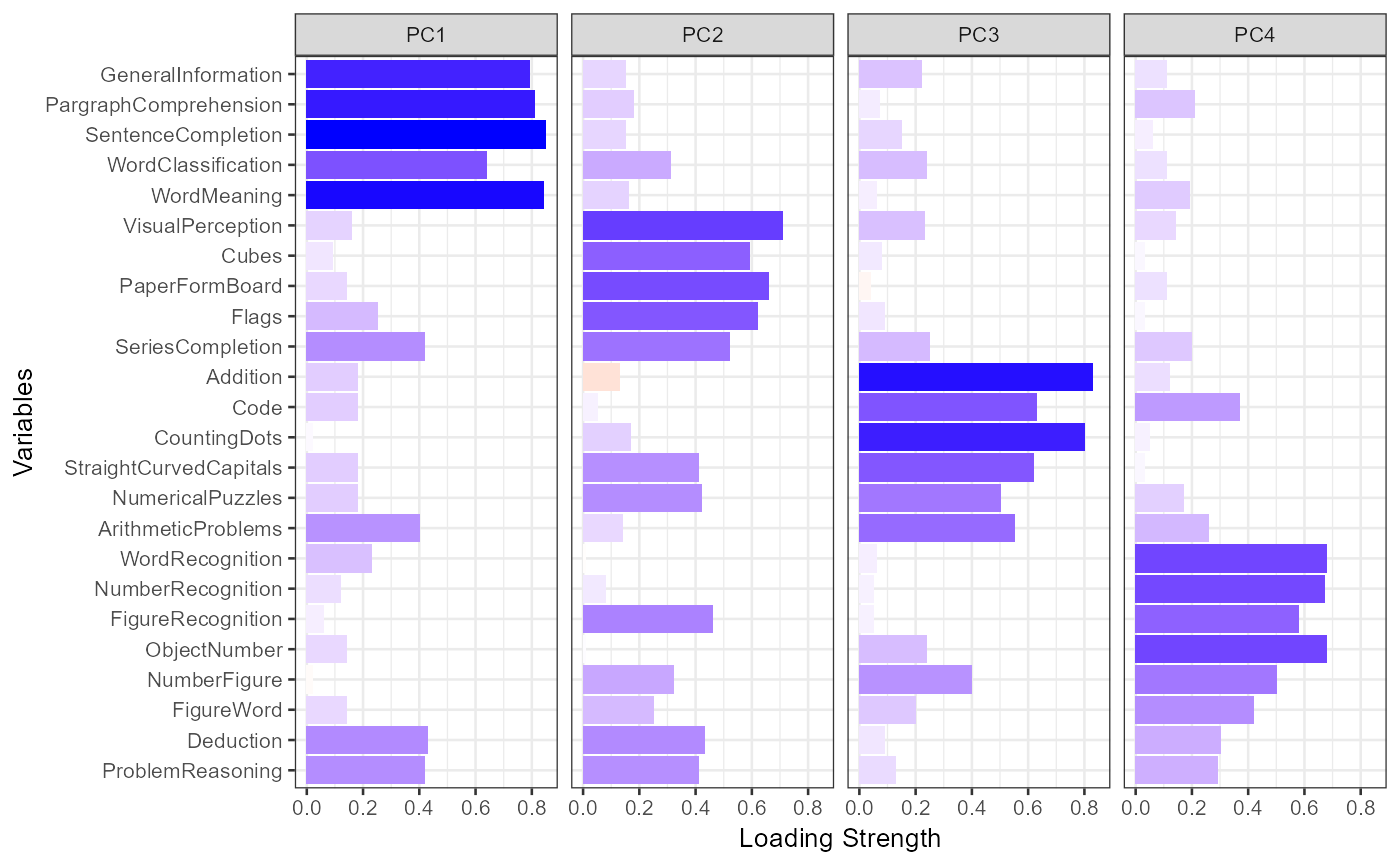
fit.pca <- PCA(Harman74.cor$cov, nfactors=4, rotate="varimax")

#> 
#> Principal Components Analysis
#> Number of Factors: 4 Rotation: varimax 
#> 
#> Component Structure
#>                          PC1   PC2   PC3  PC4   h2
#> VisualPerception        0.16  0.71  0.23 0.14 0.60
#> Cubes                   0.09  0.59  0.08 0.03 0.37
#> PaperFormBoard          0.14  0.66 -0.04 0.11 0.47
#> Flags                   0.25  0.62  0.09 0.03 0.45
#> GeneralInformation      0.79  0.15  0.22 0.11 0.70
#> PargraphComprehension   0.81  0.18  0.07 0.21 0.73
#> SentenceCompletion      0.85  0.15  0.15 0.06 0.77
#> WordClassification      0.64  0.31  0.24 0.11 0.57
#> WordMeaning             0.84  0.16  0.06 0.19 0.78
#> Addition                0.18 -0.13  0.83 0.12 0.76
#> Code                    0.18  0.05  0.63 0.37 0.57
#> CountingDots            0.02  0.17  0.80 0.05 0.67
#> StraightCurvedCapitals  0.18  0.41  0.62 0.03 0.59
#> WordRecognition         0.23 -0.01  0.06 0.68 0.52
#> NumberRecognition       0.12  0.08  0.05 0.67 0.48
#> FigureRecognition       0.06  0.46  0.05 0.58 0.55
#> ObjectNumber            0.14  0.01  0.24 0.68 0.54
#> NumberFigure           -0.02  0.32  0.40 0.50 0.51
#> FigureWord              0.14  0.25  0.20 0.42 0.30
#> Deduction               0.43  0.43  0.09 0.30 0.47
#> NumericalPuzzles        0.18  0.42  0.50 0.17 0.49
#> ProblemReasoning        0.42  0.41  0.13 0.29 0.45
#> SeriesCompletion        0.42  0.52  0.25 0.20 0.55
#> ArithmeticProblems      0.40  0.14  0.55 0.26 0.55
#> 
#>                    PC1  PC2  PC3  PC4
#> Variance          4.16 3.31 3.22 2.74
#> Var Explained     0.17 0.14 0.13 0.11
#> Cum Var Explained 0.17 0.31 0.45 0.56
plot(fit.pca)

plot(fit.pca, type="bar")